很多时候，我们都听到这样一句话：知识改变命运！要成才，就要好好的读书，古往今来，能成就大事业的，绝大多数都是知识分子。妈妈也常用这个来教导年幼的我们，从小就要努力学习，读好小学，好中学，好大学，找好工作，好事业，娶好媳妇！
想想确实很有道理，远的不说，就拿前阵子互联网大会上那张著名的饭局图来说：文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
图中大佬哪个不是名校的高材生，个个身价数十亿上百亿，在相关领域呼风唤雨，是不是完全能证明了那个论断：知识确实能改变命运！文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
不过一般这时候就有另外的人站出来说话了：不一定啊，你看好多大佬（李嘉诚只有小学文化，王永庆也是小学程度，日本松下创始人也是小学都没毕业啊。。。）等等，这么多有名有成就的人也不是拥有高学历才取得那么辉煌的成就，加上国内广东、福建、浙江等地的好多大老板都没怎么读书，当地小孩好多都是十来岁就不怎么读书了，一样的当老板，赚大钱。文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
怎么办？到底哪个才是正确的呢？是不是知识改变命运，又或者读书没用，不读书一样能成功。不管怎么说，似乎都能找到一堆理由。文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
要判断这个问题，其实并不难。文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
首先，问一个经常遇到的问题，为啥年年发布的社平工资会有很多人吐槽，觉得自己根本没达到，“被平均了”，那么为什么要平均？这个平均数怎么来的？怎么样平均才比较科学合理，不会让人有“被平均了”的感觉， 举例说明：文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
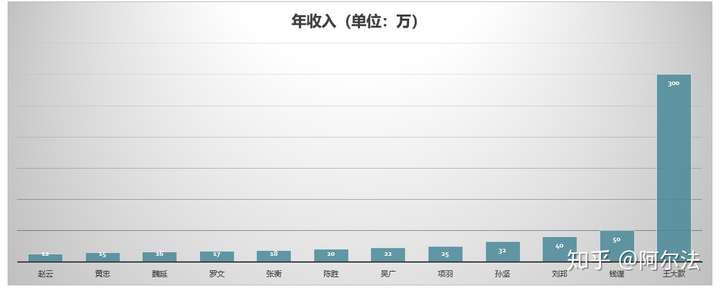
该怎么样来反映上面这些人的平均收入才合理呢？文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
如果纯粹用数字相加然后除以他们的人数的话：（12+15+16+17+18+20+22+25+32+40+50+300）/12=47.25，哇，这样下来，只有钱谨跟王大款俩人比平均值高了，很明显，其他十个人都“被平均了”，就像我们常常感觉被统计局平均的那样。那怎么办？文章源自 吾爱分享 吾爱分享网-https://www.wuaishare.cn/1795.html
这时候就要用到统计的知识了，很明显这个例子里王大款的财富相比大多数人来说太多了，拉高了平均值。那么我们用中位数显然会更合理，这里中位数为12个人收入由低往高排，处于中间位置，这里因为基数12是偶数所以是中间两个的平均值，即陈胜跟吴广俩人的平均：（20+22）/2=21，嗯，这样明显合理多了，因为王大款在这12个人里，他的收入比其他人高太多，直接除的话这个平均数就一点儿也不“平均”，那很显然作为收入来说的话，用中位数表示会更显合理。
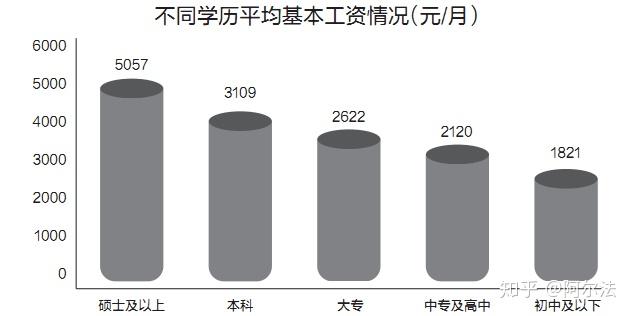
回到开头的问题，怎么看待知识改变命运这个问题。从统计学角度来说，先来看一个数据：
这个图是不同学历人群的平均收入情况，用到了中位数的概念，很明显随着学历（知识）增高，收入水平也相应的提高了，那么知识改变命运的说法也是普遍成立的。
那么怎么看待小学没有读完，却最终成功成为著名的企业家这种例子呢？包括闽粤等地方一些知名老板学历不高以及很多认为的普遍读书无用论的情况呢？
这时候，还是要用到统计学来解释了：
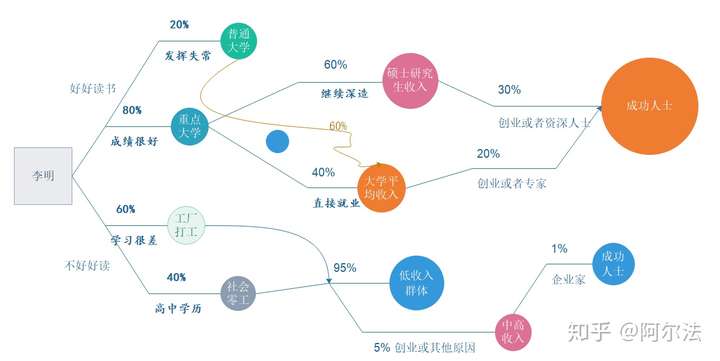
统计学有一个名词叫：概率。它指的是一个事物出现的可能性是多少。计算方式为：事情出现的情况除以总共可能的情况，比方说玩色子丢出1个点的概率就是1/6，因为它有6个面，总共会出现六种结果。几种事情同时出现的概率是把各自概率相乘，比如说色子连续出现三个1的概率就是（1/6)*(1/6)*(1/6)=1/216，可以看到这种可能性很小很小的。那么我们用一个树状图来表示开始的问题，关于知识改变命运：
从这个图上可以看出，李明最终也能成为成功人士，即使他没有读书，但是这个概率极低：5%*1%=0.05%，那么你觉得你会是那个0.05%吗？李嘉诚毕竟不常有。或者你还是选择走另一条路，读大学，即使普通大学毕业，也依然是有20%*60%*20%=2.4%的概率能成功，即便不能成为那少数，大多也是能达到按学历来说相对更高一级的收入水平。再想想上面的乌镇精英的饭局。这样一来，关于知识改变命运这个说法还有问题吗？
知识改变命运，学好统计学就是个例子，要是你很早就明白这些统计道理，那么你必然会选择一条最容易成功的路：那就是好好的读书！
评论